En ese momento me dio la luz para escribir este post (no sabia sobre que escribir, con tantas cosas que se pueden hacer!), ya que la entrada de datos en R, es sumamente importante y teniendo claro esto, muchas de las cosas que uno hará en R serán "breves*" (como decimos los "ñeros" jejeje).
*BREVE= en el lenguaje "ñeristico", significa, fácil, sin complique, suave, etc!
Para empezar, aclarare donde deben estar nuestros archivos de datos en nuestro computador y como decirle a R, donde estan o como decirle cuando cambiar de lugar para trabajar.
Entonces, como bien sabemos en nuestro computador podriamos tener 3.548.125 carpetas en lugares como "C", "D", el Escritorio u otros dentro de estos o afuera de estos, por ejemplo:
Podría tener un archivo en formato ".txt" (mas adelante explicare lo de los formatos!) , llamado "arc_1.txt" en mi escritorio:
O podria tener otro archivo llamado "arc_2.txt" en una carpeta personal, en este caso (una carpeta mia llamada "morphometria"):
Entonces, como puedo tener archivos en muchas carpetas (no solo en estas dos), debo indicarle a R donde se encuentran los archivos que voy a utilizar en esta oportunidad; esto lo podemos hacer via linea de comandos, o lo podemos hacer graficamente.
En windows es muy sencillo hacerlo, puesto que solo se debe dar click, en "cambiar el directorio".
En linux es aun mas sencillo porque solo se debe utilizar un comando con la ruta que estemos trabajando, este comando es "setwd".
Por ejemplo, si quiero decirle que vamos a trabajar sobre el escritorio en donde esta mi archivo "arc_1.txt", le damos:
> setwd ("/home/ambrosio/Escritorio")
Y si por ejemplo, queremos trabajar en mi carpeta "morphometria", donde tengo mi archivo "arc_2.txt", solo le tenemos que indicar la ruta para acceder a la carpeta:
> setwd ("/home/ambrosio/morphometria")
Y listo!!!, de este modo le indicamos a R, donde están nuestros archivos!!
Muchas veces, a muchas personas se les hace difícil, saber la ruta, porque es una ruta muy larga o porque no la conocen, para esto solo deben pararse sobre el archivo que tenga sus datos, le dan click derecho, después le damos click a propiedades y aparecerá la ruta del archivo:
Una vez estemos en el directorio sobre el que queramos trabajar, tenemos que incluir los archivos de datos que queramos utilizar dentro de el directorio (aunque en el mismo R podemos escribir los datos con los que vamos a trabajar, como vectores, tablas, etc etc etc. pero este no es el objeto de este post, ya que estamos trabajando acerca incluir datos a R).
Para esto lo primero que tenemos que tener en cuenta son los formatos de los archivos, personalmente los archivos que yo utilizo, estan en formato .csv o .txt, es decir archivos separados por comas "," o archivos separados por espacios " ".
son muy faciles de utilizar porque pueden ser modificados en excel (para los que aman excel!!) o en editores de texto como Geany (para los que amamos geany!!) y es sencillo manejar grandes cantidades de datos con estos formatos!!!
Para aprender a crear archivos .csv y .txt he generado unos datos !IMAGINARIOS¡ acerca de algunas variables "medidas" en las 7 etapas del barrio Zapamanga de Floridablanca/Santander. Los datos fueron incluidos dentro de una tabla utilizando LibreOffice 3.3 (Abajo excel!), de allí vamos a guardarlos en formato .csv y en geany los transformaremos en formato .txt (para observar como es de fácil transformar en geany formatos sin tener que ir de nuevo a hojas de calculo y guardar en formato .txt .
Los datos originales en una tabla son estos:
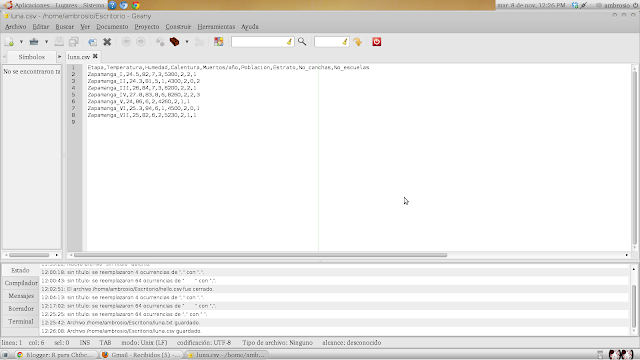
Al abrirlo en geany se vería así y no se distinguirán los decimales:
Entonces lo único que tenemos que hacer es seleccionar y copiar los datos de la hoja de calculo y pegarlos en una hoja en blanco de geany (o con el editor de texto que estemos trabajando), nos vamos a la solapa que dice "Buscar" damos clic ahi, y despues damos clic en "Reemplazar", finalmente le decimos que reemplace las comas por puntos en el documento y ya tenemos nuestros decimales definidos por puntos (ahora lo que tenemos que hacer es separar nuestras columnas por comas o por espacios, segun lo que queramos hacer (o .txt o .csv).
Para separar nuestras columnas entonces seleccionamos un espacio en blanco entre dos números:
Si hubiésemos querido el archivo en formato .txt lo unico que teniamos que hacer era reemplazar la seleccion hecha en el paso anterior por un espacio en blanco y ya!!!.
Obviamente una vez terminada nuestra edición debemos guardar el archivo en la carpeta que estemos trabajando, entonces, nos vamos en geany a "Archivo", le damos "Guardar como" y nombramos el archivo como "luna.csv" (en honor a la nueva mascota de Juancho) y sí la tenemos en formato .txt la nombramos "luna.txt". Este seria el aspecto final de los archivos en ambos formatos:
Archivo en formato .txt (luna.txt)
Archivo en formato .csv (luna.csv)
Una vez teniendo listos nuestros datos en la carpeta que estemos utilizando, los incluiremos en R, para esto necesitamos simples comandos de lectura en R, dependiendo si el formato que vamos a leer es .csv o .txt.
empezaremos llamando nuestro formato .csv
> chorizo <- read.csv("luna.csv",header=T)
#Este comando indica que crearemos un objeto con el nombre "chorizo" en R, a partir de una matriz de datos externa (nuestro "luna.csv"), para esto se utiliza la función "read.csv" y lo que indica que el nuevo objeto en R se llamara chorizo es la flecha "<-", el argumento header=T o header=TRUE, significa que la primer linea o fila de la matriz, son los nombres de las variables, de nos ser así, se tendría que poner, header=F o header=FALSE.
Para ver el nuevo objeto que hemos creado en R, solo tenemos que darle el nombre del objeto es decir "chorizo"
> chorizo
# Y veremos algo así en la ventana de R:
Para ver el nuevo objeto que hemos creado en R, solo tenemos que darle el nombre del objeto es decir "chorizo"
> chorizo
# Y veremos algo así en la ventana de R:
Etapa Temperatura Humedad Calentura Muertos.año Poblacion Estrato
1 Zapamanga_I 24.5 82 7 3 5300 2
2 Zapamanga_II 24.3 81 5 1 4300 2
3 Zapamanga_III 26.0 84 7 3 6200 2
4 Zapamanga_IV 27.8 83 8 6 8260 2
5 Zapamanga_V 24.0 86 6 2 4260 2
6 Zapamanga_VI 25.3 84 6 1 4500 2
7 Zapamanga_VII 25.0 82 6 2 5230 2
No_canchas No_escuelas
1 2 1
2 0 2
3 2 1
4 2 3
5 1 1
6 0 1
7 1 1
Después leeremos esta misma matriz de datos pero en formato .txt y utilizaremos el siguiente comando:
> galletas <- read.table("luna.txt",header=T)
#Con este comando indicamos que queremos crear un objeto en R con el nombre de "galletas", para eso utilizamos la función read.table (que es para leer archivos en formato.txt, el argumento "header=T", se utiliza de la misma forma como con la función read.csv, lo mismo que el uso de la flecha.
para ver el objeto hacemos lo mismo que hicimos antes, pero en vez de escribir en R "chorizo", escribimos "galletas" y veremos nuestros datos.
> galletas
#asi veremos los mismos datos que mostré anteriormente.
Una vez teniendo nuestros objetos creados en R, vamos a ver un poco acerca de como manejarlos y un tanto "jugar con ellos".
Primero que todo, debemos saber (si queremos!) que objetos hemos creado en R, para esto solo le damos el comando:
>objects ()
#esto nos muestra los objetos que hemos creado en R:
[1] "chorizo" "galletas"
En ocasiones necesitamos hacer analisis con solo algunas variables de las matrices, o solo necesitamos tomar algunos datos de esta; para eso podemos utilizar submatrices, que son muy facil de crear, o se pueden tomar los datos directamente an el analisis, utilizando los mismos argumentos de creacion de submatrices.
Por ejemplo si queremos tomar solo las variables temperatura y humedad, le indicamos con un comando que esas variables corresponden a las columnas 2 y 3 y el damos el comando:
> choricito<-(chorizo[,2:3])
#con esto le decimos que tome de la matriz original "chorizo" las columnas 2 y 3 y cree una submatriz llamada "choricito", asi que al darle el siguiente comando, nos aparecera la nueva mariz:
>choricito
Temperatura Humedad
1 24.5 82
2 24.3 81
3 26.0 84
4 27.8 83
5 24.0 86
6 25.3 84
7 25.0 82
Y si queremos decirle que tome las 4 primeras variables solo tenemos que darle el sigueinte comando:
>a<-(chorizo[,1:4])
>a
Etapa Temperatura Humedad Calentura
1 Zapamanga_I 24.5 82 7
2 Zapamanga_II 24.3 81 5
3 Zapamanga_III 26.0 84 7
4 Zapamanga_IV 27.8 83 8
5 Zapamanga_V 24.0 86 6
6 Zapamanga_VI 25.3 84 6
7 Zapamanga_VII 25.0 82 6
Ahora bien, esto lo realizamos para tomar el numero de columnas deseado o las variables que queramos incluir en el análisis, pero si por ejemplo queremos mas bien escoger el numero de filas o el numero de lugares a evaluar lo único que tenemos que hacer es cambiar la posición de la coma en el comando y ponerla al final, es decir:
>alto<-(chorizo[1:4,])
>alto
Etapa Temperatura Humedad Calentura Muertos.año Poblacion Estrato
1 Zapamanga_I 24.5 82 7 3 5300 2
2 Zapamanga_II 24.3 81 5 1 4300 2
3 Zapamanga_III 26.0 84 7 3 6200 2
4 Zapamanga_IV 27.8 83 8 6 8260 2
No_canchas No_escuelas
1 2 1
2 0 2
3 2 1
4 2 3
> galle<-(luna[2:4,])
>galle
> galle<-(luna[2:4,])
>galle
Etapa Temperatura Humedad Calentura Muertos.año Poblacion Estrato
2 Zapamanga_II 24.3 81 5 1 4300 2
3 Zapamanga_III 26.0 84 7 3 6200 2
4 Zapamanga_IV 27.8 83 8 6 8260 2
No_canchas No_escuelas
2 0 2
3 2 1
4 2 3
Con esta pequeña introduccion al manejo de datos en R, es muy facil empezar a hacer nuestros analisis, otra herramienta muy util en el manejo de datos son los archivos multiples tipo "Array", que explique en uno de mis post anteriores:
Array's en R
Espero que este post, haya sido de gran utilidad, especialmente para las personas que estan empezando a utilizar R.